A trivial example of the additional information that can be used to detect damage is a copy of the data. For N bytes of data, N bytes of additional information are needed.

As far as the ability to detect damage is concerned, data duplication can detect 100% of errors that damage a single bit within a packet and 100% of errors that damage up to N adjacent bytes within a packet. Data duplication can, however, miss some errors that damage two bits within a packet, namely errors that damage the same bit in the data and in the additional information.

Data duplication is an example of an additional information that has a relatively low ability to detect damage in spite of its size.

Adding a modulo sum of all bytes of data requires 1 byte of additional information for N bytes of data. Checksum can detect 100% of errors that damage a single bit within a packet. Checksum can, however, miss some errors that damage two bits within a packet.

Checksum is an example of an additional information that is simple to calculate and reasonably reliable given its size.

Adding an odd or even parity per each bit of all bytes of data requires 1 byte of additional information for N bytes of data. Parity can detect 100% of errors that damage a single bit within a packet. Parity can, however, miss some errors that damage two bits within a packet.

Parity is an example of an additional information that is simple to calculate and reasonably reliable given its size.

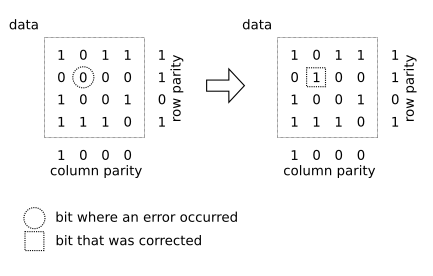
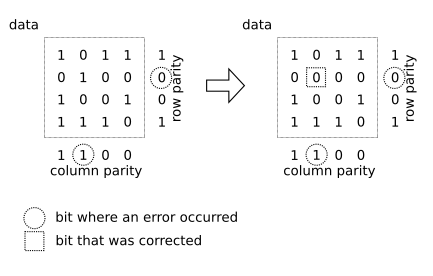
Cross parity is calculated by arranging the data in an imaginary square grid and adding an odd or even parity of all rows and all columns of data. Adding a cross parity requires 2*SQRT(N) bits of additional information for N bits of data.

Cross parity can detect 100% of errors that damage a single bit within a packet and 100% of errors that damage two bits within a packet. Cross parity can, however, miss some errors that damage three bits within a packet.

Alternatively, cross parity can be used to correct errors that damage a single bit, looking the bit up by the row and the column of the imaginary square grid that have an incorrect parity. When used to correct errors, cross parity can correct 100% of errors that damage a single bit within a packet. Cross parity can, however, mistake some errors that damage two bits for an error that damages another single bit and cause further damage rather than correct the error.

Figure 2.1. Cross Parity Correction Example

Figure 2.2. Cross Parity Miscorrection Example

Cross parity is an example of an additional information that is simple to calculate and can be used both to detect damage and correct errors.

Hamming code interleaves parity with data. Assume bits in a packet are numbered from 1. A bit at position I is a parity bit when I is a power of two, a data bit otherwise. A parity bit at position I protects groups of I bits spaced I bits apart, starting at position I.

In combination with an extra parity bit, the code can correct 100% of errors that damage a single bit within a packet and detect 100% of errors that damage two bits within a packet. Interestingly, when correcting errors, the position of a damaged bit can be calculated as a sum of positions of the parity bits that indicate the error.

Cyclic redundancy check is calculated in a modulo 2 integer arithmetic. Formally, data is interpreted as coefficients of polynomials in a commutative ring of polynomials over integers modulo 2.

When sending a data packet, the data in form of a polynomial G(x) is shifted by the width of the cyclic redundancy check and divided by a generating polynomial P(x) to form a remainder R(x) = (G(x) * x ^ DEG(P(x))) MOD P(x). The remainder R(x) is added to the data, forming the data packet F(x) = (G(x) * x ^ DEG(P(x))) + R(x). Note that in the modulo 2 integer arithmetic, both adding and subtracting the remainder yields the same result, hence the generating polynomial P(x) divides F(x).

When receiving a data packet, the packet in form of the polynomial F(x) can be damaged by an error in form of a polynomial E(x). The damaged packet F(x) + E(x) is divided by the generating polynomial P(x), yielding a remainder (F(x) + E(x)) MOD P(x) = F(x) MOD P(x) + E(x) MOD P(x) = E(x) MOD P(x). Note that the remainder depends on the error and not on the data.

The ability of the cyclic redundancy check to detect errors depends on the choice of the generating polynomial P(x). A frequent choice for the generating polynomial is x^16 + x^12 + x^5 + 1, a standard generating polynomial denoted as CCITT CRC 16. When considering errors that damage a single bit of data, E(x) has the form of x^k. Since no polynomial of the form x^k divides CCITT CRC 16 P(x), 100% of single bit errors can be detected. Similarly, it can be shown that CCITT CRC 16 can detect 100% of errors that damage any number of bits not farther apart than 16 bits and 100% of errors that damage any two bits except two bits apart exactly 2^16-1 bits. For arbitrary errors, all but one in 2^16 errors can be detected.

G = 10011101
P = 101

1001110100 DIV 101 = 10110001 (result thrown away)
 011
  111
   101
    000
     001
      010
       100
        01 = R (appended to data to form data packet)

F = 1001110101

1001110101 DIV 101 = 10110001
 011
  111
   101
    000
     001
      010
       101
        00 (indicates undamaged data packet)

E = 0001000000
F = 1001110101

1000110101 DIV 101 = 10100100
 010
  101
   001
    010
     101
      000
       001
        01 (indicates damaged data packet)

E = 0001000000

0001000000 DIV 101 = 00010101
 001
  010
   100
    010
     100
      010
       100
        01 = E MOD P = (F + E) MOD P

Cyclic redundancy check is an example of an additional information that is simple to calculate in hardware and reliable for errors that have a character of short bursts of damaged bits.

Obviously, when a correctable damage to a packet is detected, it is corrected. When an uncorrectable damage to a packet is detected, the packet is discarded and the situation is further handled as a loss of the packet. When the delays involved in handling the loss of the packet are more of a problem than size of the additional information, an additional information with high error correction ability is used so that uncorrectable damage is rare. This is called forward error correction.