To better understand what kind of process synchronization is necessary to avoid race conditions, models of synchronization problems are used. Each model depicts a particular scenario of concurrent execution and presents particular requirements on process synchronization.
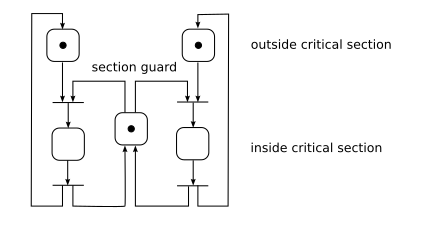
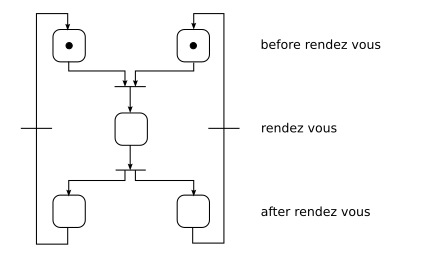
Petri nets are often used to describe the synchronization problems. Petri net consists of places and transitions. Places can hold tokens, transitions can fire by consuming input tokens and producing output tokens. Roughly, places correspond to significant process states, transitions correspond to significant changes of process state.
References. 
Carl Adam Petri: Kommunikation mit Automaten.
Mutual Exclusion models a scenario where several processes with critical sections execute concurrently. The synchronization problem requires that no two processes execute their critical sections simultaneously.
Rendez Vous models a scenario where several processes must reach a given state simultaneously.
Producer And Consumer models a scenario where several processes produce items and several processes consume items. The items are stored in a buffer of a limited size. The synchronization problem requires that the buffer neither underflows nor overflows, or, in other words, that no producer attempts to put an item into a full buffer and that no consumer attempts to get an item from an empty buffer.
Readers And Writers models a scenario where several processes write shared data and several processes read shared data. The synchronization problem requires that no two writers write the data simultaneously and that no reader reads the data while it is being written.
Dining Philosophers models a scenario where several philosophers alternatively think and dine at a round table. The table contains as many plates and forks as there are philosophers. A philosopher needs to pick two forks adjacent to his plate to dine.
The problem approximates a situation where several processes compete for an exclusive use of resources with the possibility of a deadlock.
Sleeping Barber models a scenario where several customers visit a barber in a barber shop. The shop contains a limited number of seats for waiting customers. The barber serves customers one at a time or sleeps when there are no customers. A customer enters the shop and either wakes the barber to be served immediately, or waits in a seat to be served later, or leaves when there are no free seats.
The problem approximates a situation where several processes queue to get served by another process.